Table of Contents
III. Theory and Mathematical Background – 40%
C. Discrete structures
3. Discrete probability, recurrence relations, and number theory
i. A matrix is a set of numbers arranged in two dimensions.
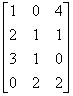
j. We calculate the product AB of two matrices A and B by producing a new matrix that has the height of the first matrix (A) and the width of the second matrix (B). We can only perform this calculation on matrices where the first matrix’s width is equal to the second matrix’s height. Each value in the new matrix is the sum of the products of each set of values in the first matrix’s row and the second matrix’s column. For example, take two matrices A and B.
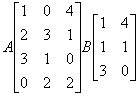
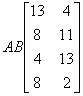
The value in the upper left hand corner of the new matrix is 1×1 + 0x1 + 4×3 = 13. The new matrix is
k. We use the modulo (mod) operator to find the remainder of a division operation. For example, 17 mod 5 is 2. When you divide 17 by 5 you get 3 remainder 2. All by itself, this is a silly operation, but it turns out that there are many applications in things like cryptography and hash tables. So, we need to know some of the special properties of modulo arithmetic. Take two integers A and B and a positive integer M. If (A-B)/M is an integer, then we say that A is congruent to B modulo M, written A º B (mod M). Furthermore, A º B (mod M) Û A mod M = B mod M. Meaning that the remainder after dividing A/M will equal the remainder of B/M. Also, A º B (mod M) Û A = B + kM, for some integer k. This is intuitive if you look closely. We already know that A º B (mod M) Û (A-B)/M. There must be some multiple of M that we can add to B to get A. Just like there are an infinite set of numbers that are divisible by M, there are an infinite set of numbers that are mod M. All of the integers that are congruent to A modulo M are in the congruence class of A modulo M. We also have some very interesting properties when we deal with congruence classes. If A º B (mod M) and C º D (mod M), then A + C º B + D (mod M) and AC º BD (mod M). The multiplication of AC and BD being congruent is intuitive. Since each factor is congruent, then the product should be congruent (remember that modulo is just weird division, and that division is just multiplication having a bad-hair day). I do not consider the addition property very intuitive. You should try a couple of problems just to see that it works. Also, here is a little proof. If A º B (mod M) then A = B + kM for some integer k. If C º D (mod M) then C = D + jM for some integer j. Therefore, B + D = (A + kM) + (C + jM). Rearrange stuff a little and you get B + D = (A + C) + (k + j)M. Remember that A º B (mod M) Û A = B + kM; treat B + D as the A, (A + C) as the B, and the (k + j) and the k, and you will see that A + C º B + D (mod M).